データ分析におけるキャリブレーション

キャリブレーションとは
クラス分類におけるキャリブレーション
キャリブレーションの評価指標
キャリブレーション方法
- Isotonic Regression
- Platt Scaling
キャリブレーション実践
まとめ
参考資料

キャリブレーションとは

Calibration(以下，キャリブレーション) とは予測モデルの誤差分布を改善するための後処理の技術になります．

機械学習のモデルを構築してシステムにインプリする前に，モデルから得られるスコア値と実測値の誤差における分布や推定がどの程度適切に行われるかを知ることは非常に重要です．そこで今回は一般的なキャリブレーション手法について記していきます．

まずはじめにクラス分類問題における評価指標とモデル出力について説明します．
クラス分類における機械学習モデルの評価指標としてはaccuracyやF値，マクロ平均などがあり，その他にもloglossやMSE，ROCAUCと言った指標が使われます．そして，これらの指標は一般的にモデルから得られる出力値である0〜1の連続値より得られます．ここで問題となってくるのがこのモデルから得られる出力値を確率とみて判断することが適切で，信頼できる確率の値となっているかということです．

ここで実世界で扱うデータを考えたときに，分類問題で扱うデータは高いインバランス性を備えたデータであることが往々にしてあります(以下で記載の図のように各クラスで偏りがある状態を指します)．そのため，我々はモデルを構築する際にアンダーサンプリングしてモデリングを実施しますが，これによってモデルにバイアスを生じさせる結果に繋がります．つまり，ここで生成されたモデルは実際の発生確率と異なるデータ分布によって学習されたモデルとなるため，予測されたスコア値が実際の発生確率の分布を近似できていない可能性が高いということです．
このように明らかにモデルの出力が実際の確率分布を捉えられていない場合もある中で，出力値を確率として扱いたい場合にはキャリブレーションによる補正が必要になってきます．ここまででキャリブレーションの必要性が理解できたところで次からは利用方法について解説していこうと思います．

キャリブレーションの評価指標

ここからはキャリブレーションの利用方法について記載していきます．
早速キャリブレーションの説明といきたいところですが，キャリブレーションを実施する前にモデルから得られたスコア値が本当にキャリブレーションが必要かどうかといった信頼性を確認する必要があります．

モデルのスコア値が信頼できる確率値となっているのかを測定する方法としては主に以下のようなものがあります．

Reliability Diagram
Expected Clivation Error(ECE)
Maximum Calibration Error(MCE)

それぞれについて簡単に説明しておきます．

Reliability Diagram

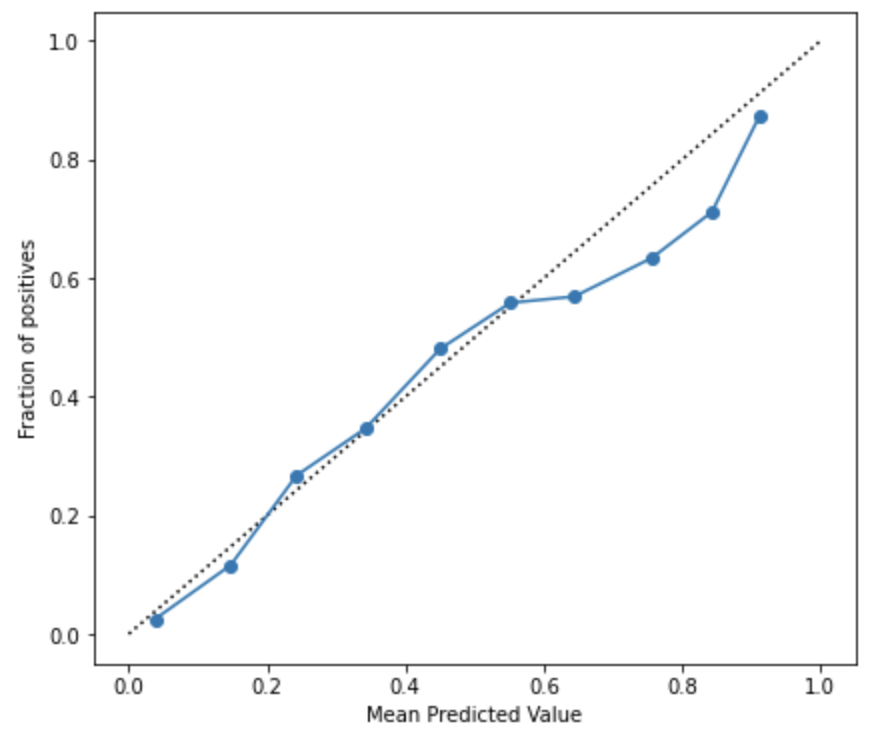
Reliability Diagramとは予測モデルによって得られたスコア値に対してプロットされた事象の観測頻度のグラフとなります．キャリブレーションの可視化では頻繁にこのグラフが用いられます．横軸にはビン毎の予測されたスコア値の平均を，縦軸には各ビン毎のポジティブなラベルの割合を示したものになります．要するに，y=x 上にプロットが近くにつれて予測値を確率として扱う信頼度が高いということが言えます．

Expected Calibration Error(ECE)

ECEはビン毎の正解ラベルの割合と予測確率の誤差に対して各ビン毎のデータ数をもとに加重平均した指標です．当然のことながらECEの値が小さい方が信頼性の高い確率予測であることを示しています．ECEは広くキャリブレーションの誤差を計測する方法として利用されていますが，最近ではECEよりも適切なキャリブレーション評価指標としていくつかの別手法を提案した論文*1も散見されていますので，問題に応じて適切な評価指標を選択していく必要があります．

$\displaystyle{ ECE = \sum_{m=1}^M \frac{|B_m|}N |acc(m) - conf(m)| \\ M : ビンの数 \\ N : 全体のサンプル数 \\ B_m : ビン内のサンプル数 \\ acc : accuracy ( 精度 ) \\ conf : 確率予測値の平均（信頼度） }$

Maximum Calibration Error(MCE)

MCEは各ビンの誤差の中で最も大きい誤差を評価する指標です．もっとも悪いシナリオの影響を最小限に抑えようとするときに役立ちます．ECEと同様に値が小さい方がより信頼性の高い確率予測であることを示します．

$\displaystyle{ MCE = max_{m\in{[1, ... , M]}} |acc(m) - conf(m)| \\ M : ビンの数 \\ acc : accuracy ( 精度 ) \\ conf : 確率予測値の平均（信頼度） }$

キャリブレーション方法

さて，本命でありますキャリブレーション方法についてです．
メジャーな手法としては以下があります．

Isotonic Regression
Plat Scaling

以下ではそれぞれについて簡単に説明していきます．

Isotonic Regression

Isotonic Regressionは2値分類に限定して利用できる手法でノンパラメトリックな手法です．非減少関数をデータに適合させます．
ノンパラメトリックな手法のため，様々な形状の Reliability Diagram において適応することができます．しかし，その反面でOverfitを避けるためにより多くのデータが必要となるといった制約が存在します．また，データ量が少ない場合には後述する Platt Scaling よりも結果が悪くなることが指摘されているため，利用の際には注意が必要です．

$\displaystyle{ y_{i} = m(f_{i}) + \epsilon_{i} \\ m : 単調増加関数 \\ f_{i} : モデルからのスコア値 \\ y_{i} : 正解ラベル }$

Platt Scaling

Platt Scalingは説明変数をモデル出力値f(x)、目的変数を正解ラベルとしてSigmoid関数にフィットさせ、そのSigmoid関数に通した値をCalibrationした値とする方法です．
一般的に，この方法はキャリブレーションされていないモデルの信頼性が低く、高出力と低出力の両方で同様のキャリブレーション誤差がある場合に最も効果を発揮します．故に境界部分を厳しく判別するSVMなどでは高い効果が得られるようです．
また，Isotonic Regression との住み分けですが，Platt Scaling は、Reliability Diagram がSigmoid形状である場合にのみ大きく作用することから、Sigmoid形状以外の場合ははIsotonic Regressionを使用するのが良さそうです．

$\displaystyle{ P(y=1|x) = \frac{1}{1+exp^{Af(x)+B}}\\ f(x) : 分類器から得られるスコア値 \\ A, B : 最急降下法等から得られる推定値 \\ }$

ここでは頻繁に出てくるキャリブレーション手法を取り上げましたが，記載した2つの手法以外にもニューラルネットワークに特化してキャリブレーションする手法*2などもありますのでさらに別の手法を知りたい方はそちらも参考にしてみてください．
では，ここまででキャリブレーションにおける指標と手法について述べてきたので具体的な実装方法について以下では記載していきます．

キャリブレーション実践

公開データセットを用いて予測モデルの構築と推論を行って取得したスコア値に対して Reliability Diagram の確認とキャリブレーション実施後の Reliability Diagram の変化を確認していきます．

動作環境

実行環境は以下となっています．

$ sw_vers
ProductName:    Mac OS X
ProductVersion: 10.14.6
BuildVersion:   18G6042

$ python -V
Python 3.9.1

利用データ

今回利用するデータはこちらのKaggleで公開されている「Telco Customer Churn」のデータセットです．

www.kaggle.com

このデータセットは説明変数として顧客毎のインターネット利用やサポートなどのサービス利用有無のデータが含まれており，目的変数はChurnと呼ばれるカラムで顧客が先月中に退会したかどうかを示すフラグとなっています．以下ではこのデータを用いて顧客が退会するかどうかの2値分類のタスクを考えてモデルを構築していきます．加えて，その過程でキャリブレーションについても同様に実施していきます．

実装例

まずは通常のモデリングと同様に予想モデルを構築して行きます．

import os
import sys
import numpy as np
import pandas as pd
import seaborn as sns
import category_encoders as ce
import matplotlib.pyplot as plt
from IPython.display import display
import lightgbm as lgb
from sklearn.metrics import auc, roc_auc_score
from sklearn.model_selection import train_test_split
from sklearn.calibration import calibration_curve

# データの読み込み
df = pd.read_csv("data/telecom/WA_Fn-UseC_-Telco-Customer-Churn.csv")
df.head()

# 前処理
df = df[df.TotalCharges != " "]
df.TotalCharges = df.TotalCharges.astype(float)
df.replace({'Churn': {"Yes": 1, 'No': 0}}, inplace=True)
df.dropna(how='any', axis=0, inplace=True)

# カテゴリ変数のエンコード
encode_cols = [
    'gender', 'Partner', 'Dependents','PhoneService', 'MultipleLines', 
    'InternetService', 'OnlineSecurity', 'OnlineBackup', 'DeviceProtection',
    'TechSupport', 'StreamingTV', 'StreamingMovies', 'Contract', 
    'PaperlessBilling', 'PaymentMethod',
]
ce_oe = ce.OneHotEncoder(cols=ordinal_encodes, handle_unknown='impute')
df = ce_oe.fit_transform(df)

# 学習モデル生成
target = 'Churn'
iD = 'customerID'
SEED = 40
test_size = 0.15
val_size = 0.05
predictors = [col for col in df.columns if col not in [target, iD]]
X_train, X_test, y_train, y_test = train_test_split(df[predictors], df[target],
                                                   test_size=test_size, random_state=SEED)
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train,
                                                   test_size=val_size, random_state=SEED)

lgb_m = lgb.LGBMClassifier(
    boosting_type='gbdt',
    objective='binary',
    learning_rate=0.005,
    max_depth=-1,
    num_boost_round=1000,
    lambda_l1=1,
    lambda_l2=0,
    min_child_weight=.5,
    subsample=.8,
)
lgb_m.fit(X_train, y_train)

# テストデータからのスコア計算
y_pred = lgb_m.predict_proba(X_test)[:, 1]

モデルが生成できたので精度を確認してみます．
AUCを評価指標としてROC Curveを出力します．また，ここでReliability Diagramも合わせて可視化します．

def viz_roc_curve(y_test, y_pred):
    """
    Args:
        y_test: (np.array) テストラベルのリスト
        y_pred: (np.array) 予測ラベルのリスト
    """
    fpr, tpr, thresholds = roc_curve(y_test, y_pred)
    _auc = auc(fpr, tpr)
    fig, ax = plt.subplots(figsize=(10,6))
    plt.plot(fpr, tpr, color='darkorange',label='ROC curve (area = %0.2f)' % _auc)
    plt.plot([0, 1], [0, 1], color='navy', linestyle='--')
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.05])
    plt.legend(loc="lower right")
    plt.show()


def viz_calibration_curve(y_test, y_pred, name):
    """
    Args:
        y_test: (np.array) テストラベルのリスト
        y_pred: (np.array) 予測ラベルのリスト
        name: (str) グラフタイトルに表示する文字列
    """
    frac_of_pos, mean_pred_value = calibration_curve(y_test, y_pred, n_bins=10)

    fig, ax = plt.subplots(1, 2, figsize=(15,6))
    ax[0].plot([0, 1], [0, 1], "k:", label="Perfectly calibrated")
    ax[0].plot(mean_pred_value, frac_of_pos, marker="o", label=f'{name}')
    ax[0].set_ylabel("Fraction of positives")
    ax[0].set_ylim([-0.05, 1.05])
    ax[0].legend(loc="lower right")
    ax[0].set_title(f'Calibration plot ({name})')
    
    sns.distplot(y_pred, bins=100, label='predicted score', ax=ax[1])
    ax[1].legend(loc='upper right')
    ax[1].set_xlim([-0.05, 1.05])
    plt.show()

# AUCとReliability Diagramの可視化
viz_roc_curve(y_test, y_pred_test)
viz_calibration_curve(y_test, y_pred, 'lightgbm')

AUCは85%となっており，まずまずの精度が出ていることを確認しました．

Reliability Diagramはスコア値が高くなるに連れて誤差が大きくなっていますが，スコア値を確率として扱うことに関して概ね乖離はなさそうに見えます．
いろいろ調べていくとLightGBMの2値分類ではloglossを最適化することからキャリブレーションは必要ないと言う内容の記事も散見されました．loglossでは誤差の幅も考慮されることから実測と予測が乖離しているほどペナルティーが加算されるため，学習が進むにつれて予測が高い確度で当てられるものはスコア値が高くなるため実際の確率に近しくなっていくことは感覚と近しい部分があります．ですが，必ずしもキャリブレーションを実施しなくても良いとは言い切れないので，必要に応じてReliability Diagramを可視化して確認する方が良いでしょう．

続いて学習時のアルゴリズムをSVMにして精度とReliability Diagramを確認していきましょう．

from sklearn.svm import SVC

# SVMでのモデル学習
svc = SVC(max_iter=10000, probability=True)
preds_svc = svc.fit(X_train, y_train).predict(X_test)

# テストデータからのスコア計算
probs_svc = svc.decision_function(X_test)
pred_svc = (probs_svc - probs_svc.min()) / (probs_svc.max() - probs_svc.min())

# AUCとReliability Diagramの可視化
viz_roc_curve(y_test, pred_svc)
viz_calibration_curve(y_test, pred_svc, 'SVM')

SVMではAUCが79%となりました．
LightGBMと比べると精度が落ちていますが，そこそこの精度が出ていますね．

続いてReliability Diagramですが，先ほどのLightGBMと比べてReliability Diagramがかなりスコア値が確率と乖離があるようになりました．全体的にスコア値が実際の確率よりも少し高めになっている様子が見受けられます．
では，このSVMのモデルをisotonic regressionとPlatt Scalingの2つの手法でキャリブレーションしてみます．

from sklearn.calibration import CalibratedClassifierCV

# Isotonic Regressionでのキャリブレーション
isotonic = CalibratedClassifierCV(svc, cv=5, method='isotonic')
isotonic.fit(X_train, y_train)
pred_svc_isotonic = isotonic.predict_proba(X_test)[:,1]

# Platt Scalingでのキャリブレーション
platts_scaling = CalibratedClassifierCV(svc, cv=5, method='sigmoid')
platts_scaling.fit(X_train, y_train)
pred_svc_platt = platts_scaling.predict_proba(X_test)[:,1]

# AUCとReliability Diagramの可視化
viz_calibration_curve(y_test, pred_svc_isotonic, 'SVM [isotonic]')
viz_calibration_curve(y_test, pred_svc_platt, 'SVM [platt scaling]')

キャリブレーションの実装自体はscikit-learnのCalibratedClassifierCV クラスにて実装されているので利用自体はとても簡単です．Isotonic Regressionと Platt Scaling の使い分けはパラメータで指定するだけですので分かりやすいですね．

Isotonic Regressionではキャリブレーション前のReliability Diagramよりも低いスコア値の場合が適切に補正されているのが見てとれます．
一方で高いスコア値の場合はキャリブレーション前よりは改善していますが，低いスコア値の時に比べると若干の誤差が生じているようです．

Platt Scalingでも同様に低いスコア値の時は確率として扱っても問題なさそうですが，一方で高いスコア値の時は確率が高めに見積もられてしまっているようです．とは言え，キャリブレーションを適応することでスコア値を確率として扱うための補正が行えることが分かりました．

まとめ

今回はKaggleのデータセットを題材として，スコア値を確率として扱う信頼性の確認方法からスコア値を確率として扱うためのキャリブレーションについて説明しました．
最近ではニューラルネットワークでキャリブレーションを扱う手法やECEやMEC以外の新しい評価指標も提案されていたりするのでこちらも継続して情報をアップデートする必要がありそうです．データ分析では前処理やモデル構築の部分がフィーチャーされがちですが，こういった後処理部分でもまだまだ学ぶべき項目がたくさんありますね．機械学習つよつよエンジニアへの道のりは長いですが継続して今後も精進していきましょう．

takaheroxにOFUSEする